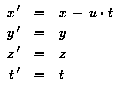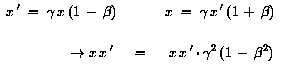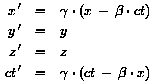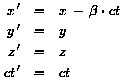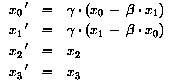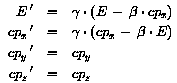Die Aussagen des letzten Kapitels lauteten:
-
Es existiert kein ausgezeichnetes Inertialsystem IS,
-
Inertialsysteme unterscheiden sich gegenseitig nur durch ihre Relativgeschwindigkeit
u.
Daraus ergab sich die Transformationsgleichung zwischen Inertialsystemen
(Galilei-Transformation):
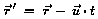 Wir wollen zur Vereinfachung der Schreibweise jetzt das Koordinatensystem
so drehen, daß die x-Achse in Richtung von u zeigt. Dann lautet
allgemein die Galilei-Transformation
Wir wollen zur Vereinfachung der Schreibweise jetzt das Koordinatensystem
so drehen, daß die x-Achse in Richtung von u zeigt. Dann lautet
allgemein die Galilei-Transformation
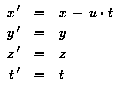 Jetzt ist auch die Zeit mit einbezogen! Die Galilei-Transformation nimmt
nämlich stillschweigend an, daß t in allen IS
gleich schnell abläuft, denn sonst würde
Jetzt ist auch die Zeit mit einbezogen! Die Galilei-Transformation nimmt
nämlich stillschweigend an, daß t in allen IS
gleich schnell abläuft, denn sonst würde
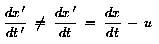 sein.
sein.
Läßt sich das experimentell überprüfen? (Man sollte
nie
physikalische Gesetze ohne experimentelle Prüfung akzeptieren!)
Experimentelle Prüfung bei kleinen
Geschwindigkeiten  (c = Lichtgeschwindigkeit):
(c = Lichtgeschwindigkeit):
Solch ein Experiment kann jeder selbst durchführen. Halte einen
Bleistift mit der Hand (IS) auf ein Papier, und bewege mit der anderen
Hand (IS') das Papier mit gleichförmiger Geschwindigkeit u
unter
dem Bleistift weg. Die Länge dx' des Strichs, den der Bleistift
im Zeitintervall dt auf das Papier (IS') gezeichnet hat,
ist gleichlang aber von umgekehrter Richtung wie die Strecke, die das Papier
im System IS zurückgelegt hat:
 -> offensichtliche experimentelle Bestätigung der Galilei-Transformation.
-> offensichtliche experimentelle Bestätigung der Galilei-Transformation.
Experimentelle Prüfung bei großen Geschwindigkeiten 
Es ist klar, daß wir obiges Experiment nicht bei den geforderten
hohen Geschwindigkeiten durchführen können (einer der Gründe,
warum uns die spezielle Relativitätstheorie so wirklichkeitsfremd
erscheint). Aber mit heutigen Beschleunigern, die Teilchen auf fast Lichtgeschwindigkeit
beschleunigen, sind solche Experimente möglich:
Am instruktivsten: Elektromagnetischer Zerfall des neutralen 
Unabhängig von der Geschwindigkeit u der Pionen legen die
2 "Lichtquanten" in gleichen Zeitintervallen immer gleiche Strecken
zurück.
Wir hatten erwartet:
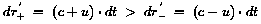 -> offensichtlicher experimenteller Widerspruch zur Galilei-Transformation.
-> offensichtlicher experimenteller Widerspruch zur Galilei-Transformation.
Folgerung, da die Lichtgeschwindigkeit offensichtlich unabhängig
von der Relativgeschwindigkeit u zwischen den Inertialsystemen ist:
|
Die Lichtgeschwindigkeit hat in allen Inertialsystemen denselben
Wert c.
|
|
Die spezielle Relativitätstheorie wurde 1905 von A.
Einstein entwickelt.
Seine erste Veröffentlichung in den
"Annalen der Physik"
trägt den Titel:
"Zur Elektrodynamik bewegter Körper"
Dies zeigt, daß sich elektromagnetische Phänomene (z.B. Licht)
besonders gut zur Verifikation dieser grundlegenden Theorie eignen. |
Der experimentelle Nachweis über die Konstanz der Lichtgeschwindigkeit
wurde erstmals von
Michelson und Morley, 1887
durchgeführt.
Ein ähnliches Experiment führen wir auch durch:
 Michelson-Morley
Experiment im Hörsaal Michelson-Morley
Experiment im Hörsaal
Am leichtesten verständlich ist ein Experiment mit neutralen 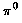 -Mesonen,
das unten skizziert ist: -Mesonen,
das unten skizziert ist:
Das  zerfällt
in 2 zerfällt
in 2  Quanten,
die im System IS' (lab-System) nachgewiesen werden. Im Eigensystem
(IS) des Pions werden die beiden Quanten,
die im System IS' (lab-System) nachgewiesen werden. Im Eigensystem
(IS) des Pions werden die beiden 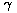 Quanten
kollinear (wegen der Impulserhaltung!) mit den Geschwindigkeiten c
emittiert. Der Effekt ist am überzeugensten, wenn man die Fluggeschwindigkeit
u
des Quanten
kollinear (wegen der Impulserhaltung!) mit den Geschwindigkeiten c
emittiert. Der Effekt ist am überzeugensten, wenn man die Fluggeschwindigkeit
u
des 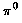 im lab-System
so wählt, daß sie die gleiche Richtung wie c hat. Dann
erwartet man für den Weg dr', den die im lab-System
so wählt, daß sie die gleiche Richtung wie c hat. Dann
erwartet man für den Weg dr', den die 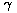 Quanten
im Zeitintervall dt im lab-System zurücklegen (beachte dr
= c · dt im Eigensystem des Pions): Quanten
im Zeitintervall dt im lab-System zurücklegen (beachte dr
= c · dt im Eigensystem des Pions):
dr+' = (c + u) · dt und dr-'
= (c - u) · dt
oder wenn beide Detektoren gleich weit vom Zerfallsort entfernt sind
(was experimentell einfacher ist) eine Zeitdifferenz im Nachweis von
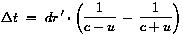 .
Dies wird nicht beobachtet, sondern es ist immer (auch wenn die .
Dies wird nicht beobachtet, sondern es ist immer (auch wenn die 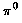 beliebige
Geschwindigkeiten haben): beliebige
Geschwindigkeiten haben):
|
Zur Erweiterung der Galilei-Transformation benutzten wir genau diese
Beobachtung:
x
= c · t aber
auch x' = c ·
t '
Wir vermeiden also auch die (ungeprüfte) Behauptung, daß die
Zeit in allen IS gleich schnell abläuft. Das IS hat
gegen das
IS' die Relativgeschwindigkeit u, das IS'
hat gegen das IS die Relativgeschwindigkeit -u.
Eine naheliegende Erweiterung der Galilei-Transformation besteht darin,
sie mit einem Faktor 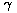 zu
multiplizieren, der für kleine Relativgeschwindigkeiten gegen 1 gehen
muß. zu
multiplizieren, der für kleine Relativgeschwindigkeiten gegen 1 gehen
muß.
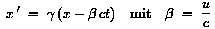 und ebenso
und ebenso
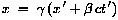 Für die Ausbreitung mit Lichtgeschwindigkeit (z.B. der
Für die Ausbreitung mit Lichtgeschwindigkeit (z.B. der 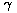 beim
beim 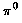 -Zerfall)
ergibt sich im IS und IS': -Zerfall)
ergibt sich im IS und IS':
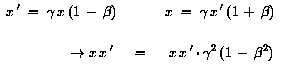 Also ist
Wegen
Also ist
Wegen 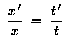 gilt
die äquivalente Transformation auch für die Zeit: gilt
die äquivalente Transformation auch für die Zeit:
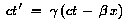
|
Die Geschwindigkeit, mit der sich ein Körper in dem Inertialsystem
IS
bewegt, ist weiterhin definiert als
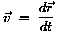 Derselbe Körper, vom System IS' aus gesehen, das sich relativ
zu IS mit u bewegt, hat die Geschwindigkeit
Derselbe Körper, vom System IS' aus gesehen, das sich relativ
zu IS mit u bewegt, hat die Geschwindigkeit
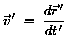 Wie hängt
Wie hängt 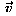 mit
mit 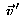 zusammen? zusammen?
Dieser Zusammenhang ergibt sich unmittelbar aus den obigen Definitionen
und der Lorentz-Transformation (nach einer etwas länglichen Rechnung)
zu:
Additionstheorem der Geschwindigkeiten:
Wichtig:
Falls 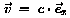 ,
dann ergibt sich ,
dann ergibt sich
 -> Die Lichtgeschwindigkeit hat in allen Inertialsystemen denselben Wert.
Dies war der Ausgangspunkt für die Herleitung der Lorentz-Transformation,
aber es ist gut zu sehen, daß diese Transformation in der Tat auch
diese Forderung erfüllt.
-> Die Lichtgeschwindigkeit hat in allen Inertialsystemen denselben Wert.
Dies war der Ausgangspunkt für die Herleitung der Lorentz-Transformation,
aber es ist gut zu sehen, daß diese Transformation in der Tat auch
diese Forderung erfüllt. |
Wir haben somit eine Transformation zwischen Inertialsystemen erhalten,
die eine konstante Lichtgeschwindigkeit in allen Inertialsystemen garantiert,
und die für kleine Relativgeschwindigkeiten u ( )
in die Galilei-Transformtion übergeht. )
in die Galilei-Transformtion übergeht. |
|
Lorentz-Transformation
|
Galilei-Transformation
|
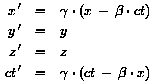
|
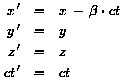
|
| Kommentare:
1.Die Zeit tritt neben dem Ort als gleichberechtigte Größe
in den Lorentz-Transformationen auf -> Ende der absoluten Zeit. Man spricht
von einem 4-dimensionalen Raum-Zeit Kontinuum, dem Minkowski-Raum.
2. Die Transformationgleichungen für IS -> IS' sind identisch
zu denen für IS' -> IS, wenn 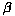 durch -
durch -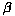 ersetzt
wird. ersetzt
wird.
3. Die maximale Relativgeschwindigkeit, die ein Inertialsystem besitzen
kann, ist 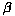 = 1 (d.h. u = c). Für Geschwindigkeiten
= 1 (d.h. u = c). Für Geschwindigkeiten 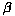 > 1 wird die Meßgröße
> 1 wird die Meßgröße 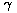 imaginär: Dies ist unmöglich! c ist daher auch für
jeden Körper prinzipiell die maximal erreichbare Geschwindigkeit.
imaginär: Dies ist unmöglich! c ist daher auch für
jeden Körper prinzipiell die maximal erreichbare Geschwindigkeit.
Wichtige Folgerungen aus der Lorentz-Transformation sind:
Zeitdilatation und Längenkontraktion (siehe rechte
Seite)
Und jetzt einige Simulationen, bei denen diese Effekte sichtbar werden:
 Simulation
relat. Effekte online Simulation
relat. Effekte online
 Simulation
relat. Effekte online Simulation
relat. Effekte online
|
1. Zeitdilatation
Wir betrachten ein Zeitintervall  im Ruhesystem IS der Uhr (x2 = x1).
Das entsprechende Zeitintervall
im Ruhesystem IS der Uhr (x2 = x1).
Das entsprechende Zeitintervall 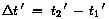 '
in einem dazu bewegten System IS' ist: '
in einem dazu bewegten System IS' ist:
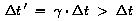
|
Das Zeitintervall Delta t im Ruhesystem der Uhr erscheint in
einem zur Uhr bewegten Inertialsystem vergrößert: "Bewegte Uhren
gehen langsamer" -> Zeitdilatation.
|
2. Längenkontraktion
Das Längenintervall in einem zum Ruhesystem IS des Maßstabs
bewegten Inertialsystem beträgt  für t2' = t1' (Messung von x1',x2'
erfolgt gleichzeitig in IS').
für t2' = t1' (Messung von x1',x2'
erfolgt gleichzeitig in IS').
Das entsprechende Längenintervall  in
IS
ist daher: in
IS
ist daher:

|
Das Längenintervall Delta x im Ruhesystem eines Maßstabs
erscheint in einem zum Maßstab bewegten Inertialsystem verkleinert:
"Bewegte Maßstäbe erscheinen verkürzt" -> Längenkontraktion.
|
Haben Sie's gemerkt: Der Unterschied zwischen beiden Aussagen wird
durch die unterschiedliche Spezifikation von Gleichortigkeit (IS)
und Gleichzeitigkeit (IS') hervorgerufen.
Diese Folgerungen sind durch die Höhenstrahlung
experimentell bestätigt (Beta-Zerfall des Myons).
|
Die Aussage über die maximale Geschwindigkeit aller Körper
bedarf der experimentellen Bestätigung. Diese ist, wegen ihrer
kleinen Masse mo = 0.0005 u, am leichtesten mit Elektronen
durchzuführen, die durch eine elektrische Kraft FC
beschleunigt werden:
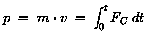 p und v, bzw
p und v, bzw 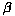 ,
können unabhängig voneinander gemessen werden. Es ergibt sich
für das Massenverhältnis ,
können unabhängig voneinander gemessen werden. Es ergibt sich
für das Massenverhältnis
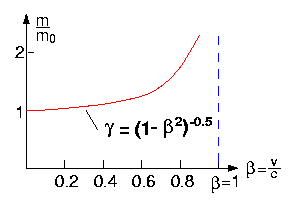
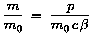 Das Ergebnis ist auf der linken Seite dargestellt.
Das Ergebnis ist auf der linken Seite dargestellt.
Für die relativistische Masse eines Körpers gilt:
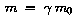
Für den relativistischen Impuls eines Teilchens gilt:

|
Beachte:
Die Vergrößerung der relativistischen Masse ist nur scheinbar
und entsteht wegen Veränderung der Raum-Zeit bei der Transformation
IS
-> IS'. Die träge Masse wird nicht verändert. |
-
Für die gemessene Geschwindigkeit gilt v
< c .
-
Die gemessene Masse m wird mit v größer:
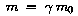
|
Man bezeichnet m0
als die Ruhemasse eines Teilchens für v = 0.Für
die relativistische kinetische Energie eines Teilchens gilt:
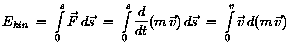 Dies ergibt nach einer etwas länglichen Rechnung, nachdem man den
Ausdruck für die relativistische Masse eingesetzt hat:
Dies ergibt nach einer etwas länglichen Rechnung, nachdem man den
Ausdruck für die relativistische Masse eingesetzt hat:
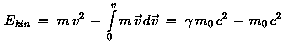
Man bezeichnet als die relativistische Gesamtenergie eines Teilchens,
als die relativistische Gesamtenergie eines Teilchens,
die Ruheenergie eines Teilchens ist 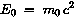 . .
|
|
| Daraus ergibt sich:
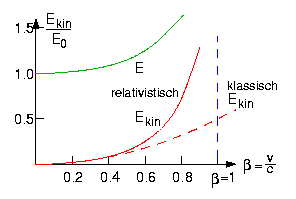
Ekin = E - E0
Das Verhalten von E und Ekin sind links dargestellt.
E = mc2
ist wohl eine der bekanntesten physikalischen Gleichungen in der Welt.
Sie besagt, daß jeder Masse eine Energie entspricht, die z.B. in
dem Gesetz von der Energieerhaltung mit berücksichtigt werden muß.
Die "Atombombe" ist wohl der experimentelle Gültigkeitsnachweis,
der jedem bekannt ist. |
 In der klassischen Näherung (
In der klassischen Näherung (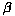 -> 0) gilt
-> 0) gilt
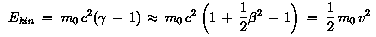
d.h. wir erhalten den klassischen Ausdruck für
Ekin! |
Die relativistische Gesamtenergie kann auch durch den relativistischen
Impuls ausgedrückt werden. Es gilt:
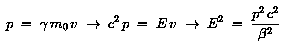 Es ist (nachrechnen mit Hilfe von
Es ist (nachrechnen mit Hilfe von 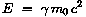 ) )
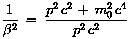 ->
->
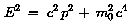
oder
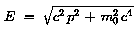
|
Wir verlassen nach unserem kurzen Ausflug wieder die spezielle Relativitätstheorie,
denn das Ziel dieser Vorlesung ist erreicht: |
Beachte folgende Äquivalenz:
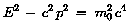 ist invariant gegen Lorentz-Transformationen
ist invariant gegen Lorentz-Transformationen
(m0 = Ruhemasse, "Teilchen ruht")
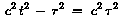 ist invariant gegen Lorentz-Transformationen
ist invariant gegen Lorentz-Transformationen
(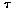 = Eigenzeit,
"Uhr ruht") = Eigenzeit,
"Uhr ruht")
-> 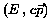 ist
Vierervektor
im
Minkowski-Raum ist
Vierervektor
im
Minkowski-Raum
-> 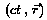 ist Vierervektor im Minkowski-Raum
ist Vierervektor im Minkowski-Raum
Die Quadrate von Vierervektoren 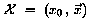 sind Lorentz-invariant, wenn
sind Lorentz-invariant, wenn 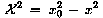
|
Die Lorentz-Transformation zwischen Vierervektoren lautet
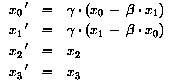 insbesondere für den Energie-Impuls-Vierervektor
insbesondere für den Energie-Impuls-Vierervektor
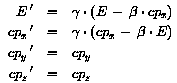
|
-
Das Konzept der Inertialsysteme gilt weiterhin: Die physikalischen Gesetze
sing gültig in allen Inertialsystemen.
-
Physikalische Größen werden von einem zum anderen Inertialsystem
mit Hilfe der Lorentz-Transformation übertragen.
-
Die Galilei-Transformation stellt die Näherung der Lorentz-Transformation
für kleine Relativgeschwindigkeiten dar.
Die Folgerungen:
-
Die physikalischen Gesetze müssen in einem 4-dimensionalen Raum (Minkowski-Raum)
formuliert werden.
-
Physikalische Größen entsprechen Vierervektoren im Minkowski-Raum,
deren Quadrate Lorentz-invariant sind.
Unsere Aufgabe wäre jetzt, zu den bisher bekannten Größen
die entsprechenden Vierervektoren zu finden, und die physikalischen Gesetze
durch Verknüpfung von Vierervektoren so zu formulieren, daß
sie konsistent mit der Lorentz-Transformation werden. Diese Aufgabe geht
über den Stoff dieser Vorlesung hinaus. Wir betrachten daher von jetzt
ab nur solche Naturvorgänge, bei denen die Relativgeschwindigkeiten
genügend klein sind -> klassische Physik. Wir werden uns aber
in der Vorlesung "Physik2" noch einmal ausführlich mit der speziellen
Relativitätstheorie beschäftigen: Magnetische Felder entstehen
durch Transformationen zwischen Inertialsystemen aus elektrischen Feldern,
und umgekehrt. |